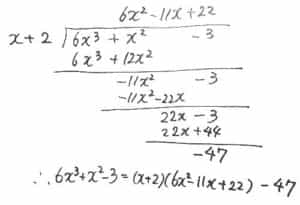【整理】多項式の割り算

多項式の割り算について整理したいと思います。通常の「変数を持たない割り算」と同じように「商」と「余り」の形を求めるものです。
変数を持たない割り算
262 ÷ 3 を行うとすると、262の中に3がいくつあるか?の答えが「商」、端数が「余り」。頭の中で計算すると、棒倒しスタイルで3の倍数をどんどん引いていくのが楽ですね。
1. 3 × 80 = 240を引く形であまり22
2. 3 × 7 = 21を更に引いてあまり1
3. よって、80 + 7 = 87が商で1が余り。
式で書くと、262=3×87+1の形になります。
4. 小数点第一位まで求めるなら、同じ発想で3 × 0.3 = 0.9を更に引いて余り0.1。
262 = 3 × 87.3 + 0.1です。
多項式の割り算
多項式も変数なしのときと同様の発想で割り算していきます。
例えば、「(6x^3 + x^2-3) ÷ (x + 2)」を行うとします。
求めるレベルは余りにxが残らないところまで割る事にします。
1. 1番次数の高い項に注目。xを何倍したら6x^3になるか考えると、(x)×(6x^2)=6x^3になる。
(x+2) × (6x^2) = 6x^3 + 12x^2 を引く形で余りが
(6x^3+x^2-3) – (6x^3+12x^2) = -11x^2 – 3
2. xを-11x倍すれば、-11x^2になり、xの項が消える。
のでこれで引き算する。
(x + 2) × (-11x) = -11x^2 – 22xを引くと余りが
(-11x^2 – 3) – (-11x^2 – 22x) = 22x – 3
3. 同様の操作で22倍したものを引く
(22x – 3) – (22x + 44) = -47
4. 以上をまとめて、
商:6x^2 – 11x + 22
余り:-47
式:6x^3 + x^2 – 3 = (x + 2)(6x^2 – 11x + 22) – 47
となります。
割る数の次数が2より多いとき
(8x^3 + 2) ÷ (6x^2 – 1) のように割る数の次数が2より多いときの余りは割る数の次数より低い次数まで出せます。やり方は省略しますが、同様の方法で求められます。
筆算が楽
普通の割り算同様、筆算で解くと楽です。