【公理から手繰る】三角形の合同条件の証明(二辺挟角、SAS)【数学探求】
備忘録になります。三角形の合同条件って何故合同と言えるのでしょうか?
まずは「2辺とその間の角がそれぞれ等しい」二辺挟角、SASのパターンについてメモしておきます。
ここでも循環論法の罠
かなり調べましたが、余弦定理や正弦定理を用いて説明しているところもありました。ただ、私の知識ではその余弦定理や正弦定理は証明に合同条件を認める事が必要で循環論法に陥ってしまいました。
手持ちの武器は公理のみ
腑に落ちた定理はまだひとつもないので、私の持っている武器は分解しようのない、初期武器(公理)のみです。最初の村を出発した勇者のようです。底辺から頑張ります。
定義:三角形の合同
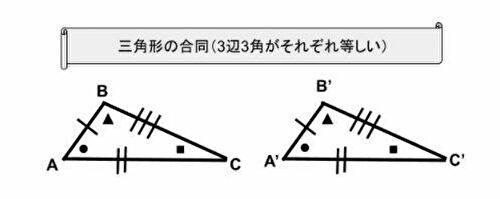
3辺3角それぞれ等しい2つの三角形を合同とする。
今回の目的
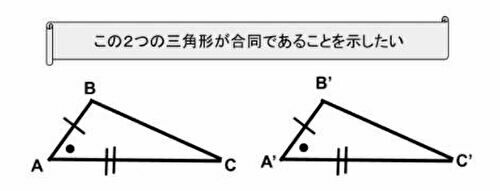
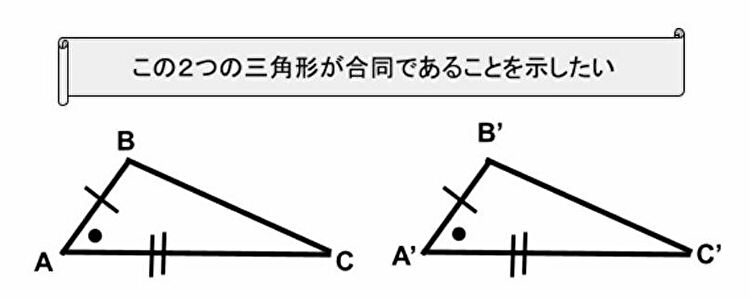
2つの三角形があって、2辺とその間の角がそれぞれ等しいケースが合同である事を導く。
使用武器(公理)の紹介
★幾何学基礎論/公理(ヒルベルト『幾何学基礎論』)
※説明は私の言いまわし(分かりやすく解釈したもの)なので、確からしい記述はリンク先を参照下さい。
公理郡Ⅲ 合同の公理4
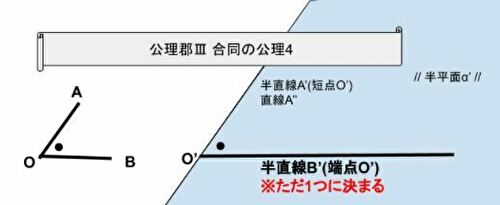
ある角AOBがあるとする。一方で点O’を端点とし、かつ直線A”に属する半直線A’があるとする。直線A”を境界とする半平面をα’とする。角AOBと合同となるような点O’を端点とする半直線B’が存在し、ただひとつに決まる。
公理郡Ⅲ 合同の公理5
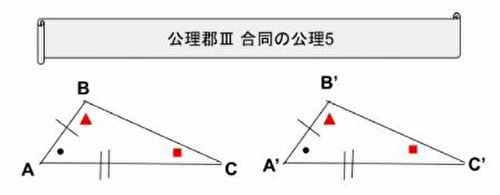
2つの三角形の2辺とその間の角がそれぞれ等しいなら別の角も等しい。
証明方法
こちらのサイトの方法が1番分かりやすかったです。詳しくはリンク先を見て頂くとして、証明の流れを書いておきます。
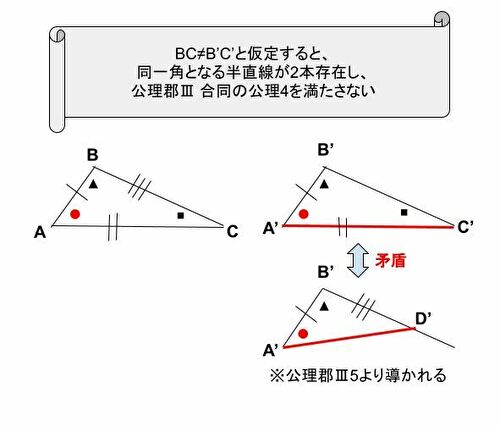
- 公理郡Ⅲ 合同の公理5により2辺と3角がそれぞれ等しいことまでは示せる。あとは残りの1辺が等しい事を示したい。
- 残りの1辺(B’C’とする)が等しくない場合、矛盾が生じる事を示す(背理法)。B’C’上に辺が等しい長さになるようなB’D’を取る。公理郡Ⅲ 合同の公理5より、角BACと角B’A’D’は等しくならなければならないが、公理郡Ⅲ 合同の公理4より等しくなる線分は1本のみとなる為、矛盾が生じる。
関連リンク