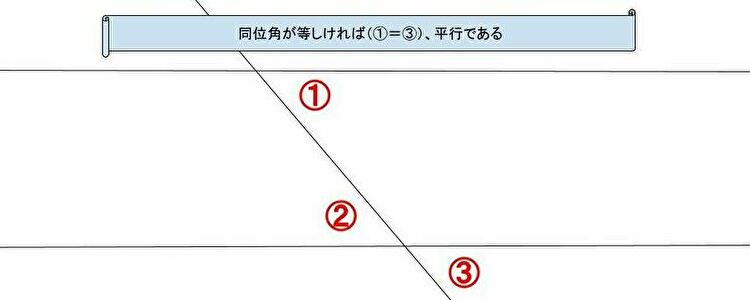
【公理から手繰る】同位角が等しければ平行の証明【数学探求】
【前回の記事はこちら】
備忘録になります。「同位角が等しければ平行の証明」を整理します。数学好きの私が調べた結果のまとめになります、ご了承下さい。
今回の目的
「同位角が等しければ平行の証明」を導きます。
平行→同位角だから同位角→平行?
過去記事にて平行→同位角は等しい事を押さえました。逆方向の流れ同位角が等しい→平行が示せるかと言えば、そうはいかなそうです。ユークリッド原論第五公準は「直線が2直線と交わるとき、同じ側の内角の和が2直角より小さい場合、その2直線が限りなく延長されたとき、内角の和が2直角より小さい側で交わる。」でありますが、「2直線が限りなく延長されても決して交わらない(=平行)な場合、同じ側の内角の和が2直角」を示している訳ではありません。必要十分条件ではなく、十分条件しか満たさないという話です。必要十分条件を示すには別のアプローチが必要です。
参考リンク
詳細はリンク先を参考にして頂ければと思います。
今回利用する確認済法則の紹介
証明の流れ
- 第2外角定理を三角形の合同条件(二辺挟角)を使って証明
- 錯角が等しい場合、直線延長上に交点がある(=平行でない)と作られる三角形において第2外角定理を満たす事が出来ず矛盾が発生する(背理法)ので、同位角が等しければ平行である
お疲れ様でした。「同位角が等しければ平行」がこれで使えます。
関連記事
外部リンク