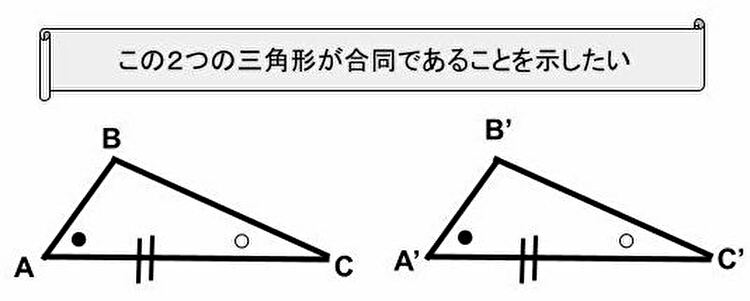
【公理から手繰る】三角形の合同条件の証明(二角挟辺、ASA)【数学探求】
【前回の記事はこちら】
三角形の合同条件って何故合同と言えるのでしょうか?前回、「2辺とその間の角がそれぞれ等しい」二辺挟角、SASのパターンを公理から示せる事が分かりました。「1辺とその両端の角がそれぞれ等しい」二角挟辺、ASAのパターンも同様に示す事が出来ます。
手持ちの武器
- 公理全般(参考リンク)
- 三角形の合同条件:二辺挟角(SAS)
やっと公理以外の武器が手に入りました。
今回の目的
2つの三角形があって、1辺とその両端の角がそれぞれ等しいケースが合同である事を導く。3角形の3辺3角がそれぞれ等しい事を示します。
使用武器(公理)の紹介
ヒルベルト『幾何学基礎論』より
※以降の説明は私の言いまわしなので、確からしい記述はリンク先を参照下さい。
公理郡Ⅲ 合同の公理4
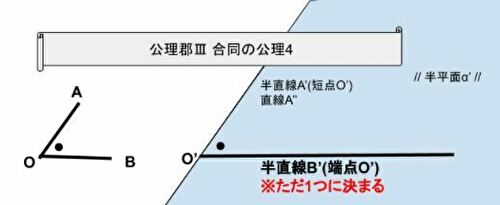
ある角AOBがあるとする。一方で点O’を端点とし、かつ直線A”に属する半直線A’があるとする。直線A”を境界とする半平面をα’に角AOBと合同となるような点O’を端点とする半直線B’が存在し、ただひとつに決まる。
公理郡Ⅲ 合同の公理5
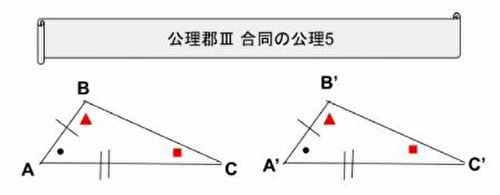
2つの三角形の2辺とその間の角がそれぞれ等しいなら別の角も等しい。(私なりの言い方で書いてます)
三角形の合同条件:二辺挟角(SAS)
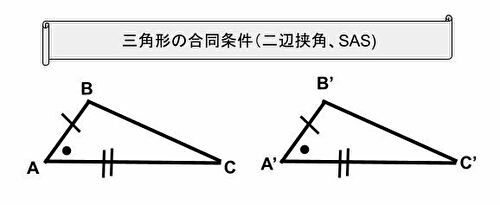
※無くても示せますが、最後端折る為に利用しました。
証明方法
ベースはSASの証明なので、その時参考にさせてもらったサイトのリンクを記載します。
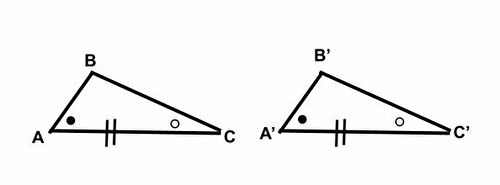
今回も証明の流れを書いておきます。三角形ABCと三角形A’B’C’の1辺(AC≡A’C’)とその両端の角(角BAC≡角B’A’C’、角BCA≡角B’C’A’)がそれぞれ等しいとします。
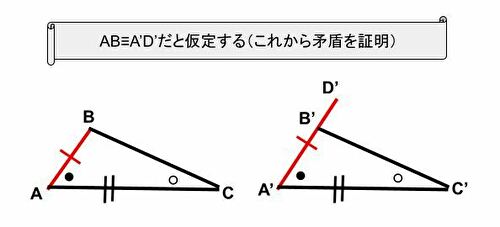
- 背理法を使います。ABとA’B’の長さが異なるとして、矛盾をこれから示します。※AB≡A’B’が示せたら、SASを満たす為、合同
- ABと長さが同じになるような線分A’D’を取ります。D’はA’B’上に取ります。
- AC≡A’C’、AB≡A’D’、角BAC≡角D’A’C’なので公理郡Ⅲ 合同の公理5により角BCAと角D’C’A’は等しくなる。
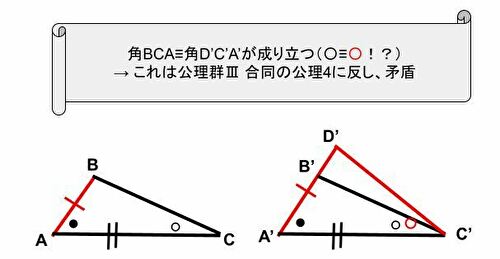
- しかし、前提条件として、角BCAと角B’C’A’は等しいため、同一直線上の1点から同一角をなす線分が複数存在することになるが、これは公理郡Ⅲ 合同の公理4に反する。よってABとA’B’の長さが異なる場合は存在せず、AB≡A’B’となる。
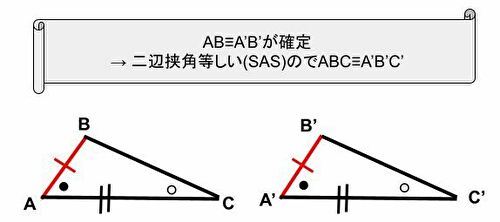
- ニ辺挟角が等しい(SAS)ため、合同である事が示された。
お疲れ様でした。これで二角挟辺(ASA)も合同条件として利用可能になりました。
関連リンク