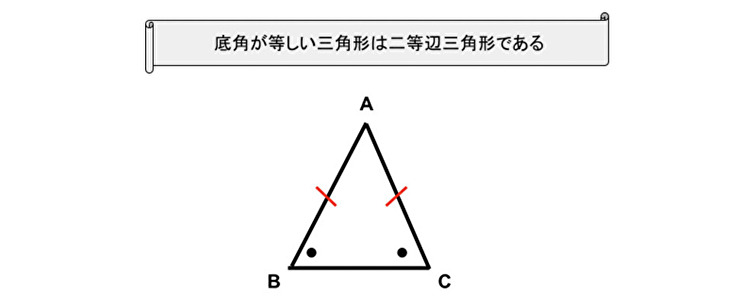
【公理から手繰る】底角が等しい三角形は二等辺三角形な証明【数学探求】
【前回の記事はこちら】
底角が等しい三角形は二等辺三角形(=二辺が等しい)である事を公理とこれまで公理から手繰り寄せた法則のみで導く流れを記載しております。公理からの流れを確認しつつ全ての定理を解き明かす記事第4回目になります。
手持ちの武器
- 公理全般(参考リンク)
- 三角形の合同条件:二辺挟角(SAS)、二角挟辺(ASA)
- 二等辺三角形の底角は等しい
ひとつずつ増やしていきます。
今回の目的
底角が等しい三角形は二等辺三角形である事を導きます。
使用武器の紹介
三角形の合同条件:二角挟辺(ASA)
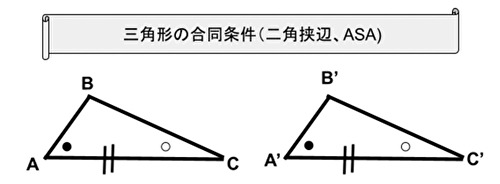
一辺とその両端の角がそれぞれ等しい三角形は合同である。
証明方法
- 底角が等しい三角形ABCと同一位置の点A’B’C’からなる三角形C’B’A’との比較を考えます。
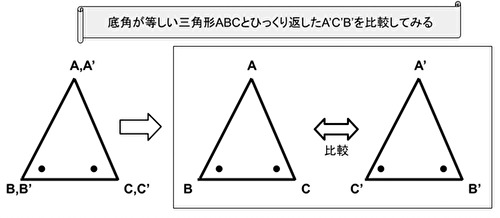
- 三角形の合同条件:二角挟辺から辺AB≡辺A’C’
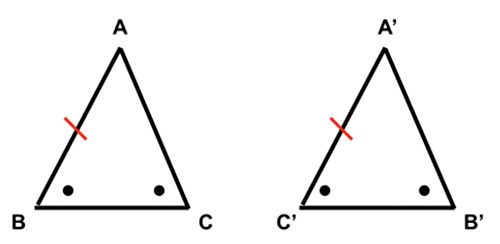
- 元々の条件から辺AC≡辺A’C’。よって辺AB≡辺A’C’≡辺ACとなり底角が等しい三角形ABCは二等辺三角形である事が証明された
お疲れ様でした。底角が等しい三角形は二等辺三角形である事がこれで使えます。
関連リンク