三角形の内角が180度の証明
頭の中整理シリーズ。三角形の内角は180度ってどうやって証明するのか編です。
ここでの前提
平行線の錯角は同じ角度であることを認める。(別で整理記事書きます)
証明
任意の三角形に補助線として平行線を引きます。
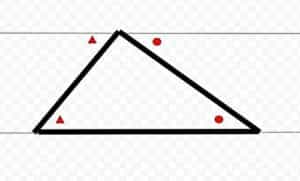
▲同士、●同士は平行線の錯角なので同じ角度。三角形の内角の和は直線の角度と等しい事が分かり、三角形の内角は180度となる。
四角形の内角が360度なのは対角線を一本引いて三角形が2つになるので180度×2=360度。五角形は三角形3つで構成されるので180度×3=540度。多角形の内角はこの方法で求められます。
関連リンク
