【公理から手繰る】三角形の合同条件の証明(三辺相等、SSS)【数学探求】
【前回の記事はこちら】
備忘録になります。合同条件のひとつ、「3辺の長さがそれぞれ等しい(3辺相等)」の証明について押さえておきます。今回も細かい点は参考にしたリンク先を見て頂くとして、理解する流れを書き記します。論理が歪まない範囲で自分にわかりやすい表現にしています。ご了承下さい。
今回の目的
「3辺の長さがそれぞれ等しい(3辺相等)」を導きます。
使用武器の紹介
参考リンク
本記事は荒い説明かと思いますので、詳細なところはリンク先を参考にして頂ければと思います。
証明の流れ
- 3辺の長さが定まった三角形は1つの形しか決まらない事を示す。
→ ユークリッド原論 第1巻命題1-7 - 3辺の長さがそれぞれ等しい2つの三角形は合同である事を示す。
原論第1巻命題1-7の概要
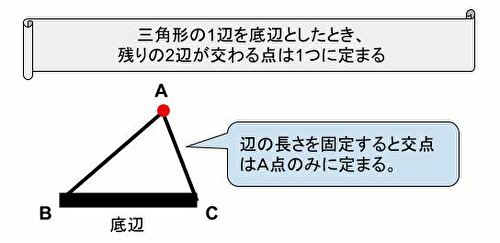
「三角形の1辺を底辺としたとき、残りの2辺が交わる点は1つに定まる」
かなり私なりの言葉で言い換えてるので原文は参考リンク先でご確認下さい。
原論第1巻命題1-7の証明
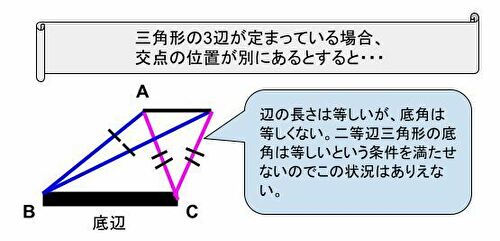
本記事では流れだけ説明します。もし他に交わる点があると仮定すると矛盾する事を示します。現在の三角形と他の交点からなる三角形が出来るとします。2つの三角形はそれぞれ、同じ長さの線分からなります。同じ長さの線分同士で三角形を見立てると、二等辺三角形が2つ出来ます。作図すると分かりやすいですが、片方では底角α<底角β、もう片方では底角α>底角βが成立しています。これは底角が等しい二等辺三角形の条件を満たしておらず、矛盾が発生します。よって、交点が複数存在することは無く、1点に定まります。
三辺相等は合同の証明
三辺の長さがそれぞれ同じ三角形の1辺を重ね合わせます。残りの2辺の交点は原論第1巻命題1-7により、1つに定まります。2線分の交点が別々の位置にはなりません。原論公理7より「互いに重なり合うものは互いに等しく」なり、三辺相等は合同という事になります。
お疲れ様でした。やっと3つの合同条件使えるようになりました。
関連リンク