【整理】平行線の同位角が等しい性質は証明不可なのか?
別記事で平行線における対頂角、錯角、同位角の話をしたのですが、「平行となる2直接を横切る1直線があり、同側の2角の和が180度になるのはそういうものなんだ」と説明不可的な感じでお話しました。そこを自分なりに深掘りしたいと思います。
参考:ウィキペディア:平行線公準
平行の大前提条件
厳密に言葉を選んでいくと、キリがなく、理解が難しすぎるところなので、あえて言葉の厳密さは気にせずに説明します。
平面にある図形の大前提条件のことを「公理や公準」と呼びます。平行線についてもこの大前提条件があり、平行線公準やユークリッドの第5公準と呼ばれます。
ユークリッド言論に書かれている第5公準の内容
「直線が2直線と交わるとき、同じ側の内角の和が2直角より小さい場合、その2直線が限りなく延長されたとき、内角の和が2直角より小さい側で交わる。」
※他の公準(例えば、点と点とで直線が引けるとかと比べて、これだけ難解な書き方なのが特徴)
平行線公準から対頂角、錯角、同位角の特徴を導く
平行線の対頂角、錯角、同位角の特徴の話をするならば、平行線公準から出発する形で証明可能です。
第5公準を逆に言うと、「直線と交わった2直線の同じ側の内角の和が2直角(=180度)であれば、2直線は交わらない(=平行)」
以下の図で平行線公準を起点に話を進めると、
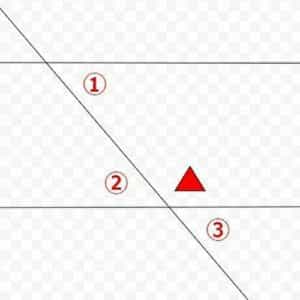
平行線における、①と▲の和は180度(平行線公準)。▲と③の和も180度(直線)なので①と③の角度は等しい。これは平行線の同位角が等しいことを示している。
併せて、対頂角となる②も角度は等しいことから、①②③は全て同じ角度となり、平行線の同位角、錯角、対頂角が等しいことが分かります。
この説明を証明と捉えて良いと思います。
平行線公準問題に対する取り組み期間はフェルマーの最終定理の比ではなかった
ウィキペディアにある、歴史の内容が面白い。この公準だけ他の公準と比べて感覚的に分かるものでは無かったので、他の4公準から導き出せるのではないかと2000年に渡って数学者が取り組んだらしい。フェルマーの最終定理が解けるまでの300年のドラマも凄いが、そのレベルではないですよね。最終的には平行線公準は他の4公準から独立したものであることが示されています。
「同値」について
他の4公準のみで説明がつかず、平行線公準の言い換えとなっている事象を「同値」と呼んでいます。「内角の和が2直角より小さい側で交わる」も「三角形の内角の和が180度」も「相似であるが合同でない三角形の組みが存在する」も同値であって、平行線公準に対する目線が違うだけ内容です。「同位角が等しい」も同値だと思います。むしろ、「平行線は同位角が等しい」を平行線公準にしてもらうほうが直感的で分かりやすいのになと感じています。
平行線公準問題で盛り上がって、非ユークリッド幾何学が誕生する
詳しい内容はウィキペディアで。これを調べていて、ユークリッドが何たるかを知れたし、非ユークリッド幾何学について、ふんわりと存在意義やニュアンスが掴めたのが嬉しかったです。
タイトルは同位角で書きましたが、元は「三角形の内角の和はなんで180度なの?」からで、そこから広がる数学の世界はまさかこんなにも深いとは思わなかったです。
関連リンク
